Introduction

Identifying asteroids that might be on a collision course with Earth is about to get a whole lot easier! Recent advancements in the mathematical modeling of gravitational light bending could revolutionize the way we track the orbits of these celestial objects with unprecedented precision.

Inspired by Historical Figures

Inspired by the pioneering work of Sir Isaac Newton and confirmed by none other than Albert Einstein, researchers have devised a refined method for determining the exact positions of minor solar system objects. This includes those pesky asteroids lurking in the Kuiper Belt—a chilling expanse filled with icy bodies including Pluto and other dwarf planets—and the far-flung Oort Cloud, suspected of housing numerous long-period comets.

New Study and Findings

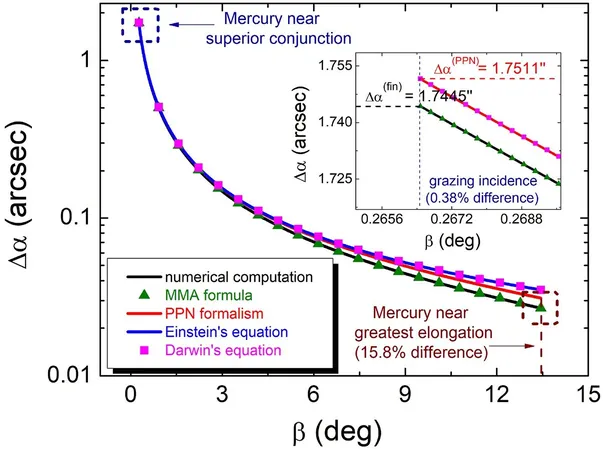
In a promising new study published in the Monthly Notices of the Royal Astronomical Society, Professor Oscar del Barco Novillo from the University of Murcia has introduced an exact equation for calculating the gravitational bending of light (GBL) angle caused by a static massive object, such as our sun or slower-moving planets.

Historical Context

Newton first introduced the concept of gravity causing the bending of light, but it was Einstein’s groundbreaking theory of general relativity, published in 1915, that brought it to life through the precise prediction of light deflection near massive celestial bodies.

Implications for Astronomy

What does this mean for astronomers? The implications are colossal! With this new equation, astronomers could accurately pinpoint the positions of asteroids and other minor objects in the solar system, enabling better orbit predictions and making it easier to spot potentially hazardous objects headed our way.

Further Applications

But that’s not all! The newfound accuracy could even enhance our understanding of Proxima Centauri, the nearest star system to us—just 4.25 light-years away—believed to be encircled by three exoplanets. Knowing its precise location could help in estimating the orbits of those planets more accurately.

Expert Insights

“Our study introduces an exact equation for calculating the GBL angle by a static massive object, making it the most accurate method to date,” Professor Novillo stated. “This has vast implications beyond just asteroids; it could refine our positioning of distant stars and enhance various branches of astronomy, such as celestial mechanics and stellar dynamics.”

Impact on Galactic Studies

The research also holds promise for more refined location tracking of distant galaxies affected by gravitational lensing, a phenomenon where the mass of galaxy clusters distorts the light from galaxies behind them. This breakthrough is crucial for astrometry, the science dedicated to measuring the positions and movements of celestial bodies with pinpoint accuracy.

Significance Amid Ongoing Missions

Moreover, this stunning advancement comes at a pivotal time as the European Space Agency’s Euclid mission gears up to produce the largest cosmic 3D map ever. Over the next six years, Euclid will observe billions of galaxies, exploring the intricate shapes, distances, and motions out to ten billion light-years—all to unveil the secrets of dark matter and dark energy that have molded our universe.

Final Remarks

Professor Novillo emphasized the paramount importance of his team's work: “The fundamental significance of our new equation lies in its exceptional accuracy for GBL angle calculations, outperforming previous post-Newtonian approximations. This research is not just an academic exercise; it has practical implications for astronomers and astrophysicists engaged in highly precise astrometry measurements, especially in the realm of gravitational lensing.

Conclusion

As we unlock the universe's mysteries, this innovative equation could very well be the key to protecting our planet from potential space threats! Stay tuned as we delve deeper into the cosmos and watch for more groundbreaking discoveries!