Após mais de 100 anos de tentativas, o enigma matemático conhecido como problema de Kakeya finalmente recebeu uma solução. A descoberta é atribuída a Hong Wang, professor da Universidade de Nova York, e Joshua Zahl, da Universidade da Colúmbia Britânica, no Canadá, que dedicaram tempo e esforço para decifrar este obstáculo que intrigava matemáticos ao redor do mundo.

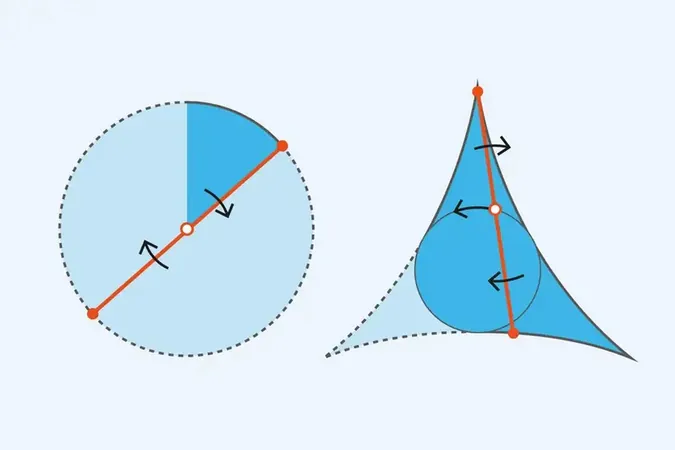
O problema em questão envolve a movimentação de uma agulha de forma a conseguir traçar um caminho que cobre todas as direções em um espaço tridimensional. Uma das abordagens para solucionar esta questão envolvia fixar uma das extremidades da agulha e girá-la em torno desse ponto, enquanto outra sugeria balanços para frente e para trás durante a rotação, o que formaria um triângulo com lados curvados.

Para que a agulha pudesse efetivamente traçar um círculo ou um triângulo, era necessário que ela estivesse em uma superfície bidimensional. Entretanto, ao se considerar um espaço tridimensional, as direções de movimento se multiplicam, tornando o problema mais complicado. Para simplificar, os pesquisadores propuseram uma agulha infinitamente fina, semelhante a uma linha, o que permitiria que ela cobrisse uma vasta gama de direções sem ocupar volume.

Embora à primeira vista a premissa possa parecer simples, a prova teórica em três dimensões levou décadas. A solução alcançada por Zahl e Wang se mostrou robusta, pois conseguiram eliminar a possibilidade de que a forma desenhada pela agulha pudesse ser menor do que três dimensões, garantindo a validade da solução para qualquer dimensão superior a três.

Curiosamente, os pesquisadores também exploraram dimensões fracionárias, como 2,5, revelando que mesmo conceitos que parecem abstratos podem ter aplicações reais na matemática moderna. Essa exploração das dimensões quebra padrões tradicionais, mas é um campo muito utilizado na análise matemática.

Com seu trabalho, a dupla confirmou que os conjuntos Kakeya não podem possuir estruturas geométricas extremamente pequenas, apesar de terem um volume tridimensional zero. Isso significa que, mesmo com uma área nula, esses conjuntos podem conter uma estrutura tridimensional intrigante. Anteriormente, em 1971, o matemático Roy Davies já havia demonstrado a possibilidade de movimentação da agulha em duas dimensões, mas a solução para três dimensões permaneceu indefinida até agora.

Um renomado matemático da Rice University, Nets Katz, afirmou que "o artigo pode ser o maior avanço da matemática do século XXI", destacando a significância da solução para um problema que foi abordado por muitos matemáticos de prestígio, muitos dos quais apenas conseguiram resultados parciais.

A solução encontrada pela equipe não apenas fecha um capítulo na matemática, mas também abre novas portas para a pesquisa em outras áreas, como física e engenharia, oferecendo uma base sólida para futuras investigações na interação entre geometria e movimento.